Ejercicio Práctico | Prueba de Hipótesis

Ejemplo

El jefe de la Biblioteca Especializada de la Facultad de Ingeniería Eléctrica y Electrónica de la UNAC manifiesta que el número promedio de lectores por día es de 350. Para confirmar o no este supuesto se controla la cantidad de lectores que utilizaron la biblioteca durante 30 días. Se considera el nivel de significancia de 0.05

Datos:

Día	Usuarios	Día	Usuarios	Día	Usuario
1	356	11	305	21	429
2	427	12	413	22	376
3	387	13	391	23	328
4	510	14	380	24	411
5	288	15	382	25	397
6	290	16	389	26	365
7	320	17	405	27	405
8	350	18	293	28	369
9	403	19	276	29	429
10	329	20	417	30	364

Solución: Se trata de un problema con una media poblacional: muestra grande y desviación estándar poblacional desconocida.

Paso 01: Seleccionamos la hipótesis nula y la hipótesis alternativa

Ho: μ═350

Ha: μ≠ 350

Paso 02: Nivel de confianza o significancia 95%

α═0.05

Paso 03: Calculamos o determinamos el valor estadístico de prueba

De los datos determinamos: que el estadístico de prueba es t, debido a que el numero de muestras es igual a 30, conocemos la media de la población, pero la desviación estándar de la población es desconocida, en este caso determinamos la desviación estándar de la muestra y la utilizamos en la formula reemplazando a la desviación estándar de la población.

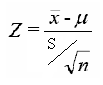
Calculamos la desviación estándar muestral y la media de la muestra empleando Excel, lo cual se muestra en el cuadro que sigue.

Columna1
Media	372.8
Error típico	9.56951578
Mediana	381
Moda	405
Desviación estándar	52.4143965
Varianza de la muestra	2747.26897
Curtosis	0.36687081
Coeficiente de asimetría	0.04706877
Rango	234
Mínimo	276
Máximo	510
Suma	11184
Cuenta	30
Nivel de confianza (95.0%)	19.571868

Paso 04: Formulación de la regla de decisión.

La regla de decisión la formulamos teniendo en cuenta que esta es una prueba de dos colas, la mitad de 0.05, es decir 0.025, esta en cada cola. el área en la que no se rechaza Ho esta entre las dos colas, es por consiguiente 0.95. El valor critico para 0.05 da un valor de Zc = 1.96.

Por consiguiente la regla de decisión: es rechazar la hipótesis nula y aceptar la hipótesis alternativa, si el valor Z calculado no queda en la región comprendida entre -1.96 y +1.96. En caso contrario no se rechaza la hipótesis nula si Z queda entre -1.96 y +1.96.

Paso 05: Toma de decisión.

En este ultimo paso comparamos el estadístico de prueba calculado mediante el Software Minitab que es igual a Z = 2.38 y lo comparamos con el valor critico de Zc = 1.96. Como el estadístico de prueba calculado cae a la derecha del valor critico de Z, se rechaza Ho. Por tanto no se confirma el supuesto del Jefe de la Biblioteca.